-2022.01~ 데이터분석 스터디 참여
-본 글에서는 <이것이 데이터 분석이다 with 파이썬> 책을 참고하여 진행한 실습(+개인적으로 더 알아본 내용)을 백업해 둠
1. 서론
비트코인 시세처럼 연속적인 시간에 따라 다르게 측정되는 데이터를 시계열 데이터라 하며, 이를 분석하는 것을 시계열 데이터(Time series analysis) 분석이라고 한다. 시계열 데이터 분석은 심작 박동 데이터처럼 규칙적 시계열 데이터를 분석하는 것과 비트코인 시세 예측처럼 불규칙적 시계열 데이터를 분석하는 것으로 구분할 수 있다.
해당 실습에서는 시계열 분석(혹은 예측)에 있어서 가장 널리 사용되는 모델인 ARIMA에 대해 알아보고 Python을 통해 구현해본다.
2. ARIMA
ARIMA는 Autoregressive Integrated Moving Average의 약자로, 전통 적인 시계열 예측 방법으로 크게 두 가지 개념을 포함하고 있다.
첫 번째는 자기 자신의 과거를 정보로 사용하는 개념이다. 이는 ‘현재의 상태는 이전의 상태를 참고해서 계산된다’라는 아이디어를 전제로 한다.
두 번째는 ‘이전 항에서의 오차를 이용하여 현재 항의 상태를 추론 하겠다’라는 방법이다. 그리고 이 둘을 합친 것을 ARMA 모델이라고 하며, 조금 더 나아간 ARIMA 모델은 ARMA 모델에 추세 변동의 경향성까지 반영한 방법이다.
ARIMA를 조금 어려운 말로 정리하면 다음과 같다.
- AR: 자기회귀(Autoregression). 이전 관측값의 오차항이 이후 관측값에 영향을 주는 모형이다. 아래 식은 제일 기본적인 AR(1) 식으로, theta는 자기상관계수, epsilon은 white noise이다. Time lag은 1이 될수도 있고 그 이상이 될 수도 있음
- I: Intgrated. 누적을 의미하는 것으로, 차분을 이용하는 시계열모형들에 붙이는 표현이라고 생각하면 편함
- MA: 이동평균(Moving Average). 관측값이 이전의 연속적인 오차항의 영향을 받는다는 모형
현실에 존재하는 시계열자료는 불안정(Non-stationary)한 경우가 많다. 그런데 기존의 모델(ARMA 등)으로는 이런 경우를 설명할 수 없다. 따라서 모델 그 자체에 비정상성을 제거하는 과정이 포함된 ARIMA를 사용하는 것이 합리적이다. 보통 ARIMA(p,d,q)로 표현한다.
ARIMA 클래스에 order=(p,d,q)라고 입력되어진 파라미터는 ‘AR이 몇 번 째 과거까지를 바라보는지에 대한 파라미터(p), 차분에 대한 파라미터 (d), MA가 몇 번째 과거까지를 바라보는지에 대한 파라미터(q)’를 의미하는 것이다.
차분이란 현재 상태의 변수에서 바로 전 상태의 변수를 빼주는 것을 의미하며, 시계열 데이터의 불규칙성을 조금이나마 보정해주는 역할을 한다. 또한 앞서 말한 ARIMA 모델의 경향성을 의미한다.
파라미터 p, d. q는 일반적인 가이드라인이 존재하는데 보통은 p와 q의 합이 2 미만인 경우, 혹은 p와 q의 곱이 0을 포함한 짝수인 경우가 좋은 파라미터의 조합이라고 알려져 있다.
3. 데이터
www.blockchain.com/ko/charts/ market-price에서 날짜와 가격이 포함된 2018년 자료를 다운받았다. CSV파일로 Export했으며, Column name만 수동으로 제거하여주었다. (str을 읽는 과정에서 error가 발생했기 때문)
4. 실습
4.1.1 시계열 정보를 데이터 프레임의 인덱스로 설정하여 가격 추이 시각화
bitcoin_df['day']=pd.to_datetime(bitcoin_df['day'])
bitcoin_df.index=bitcoin_df['day']
bitcoin_df.set_index('day',inplace=True)
bitcoin_df.plot()
plt.show()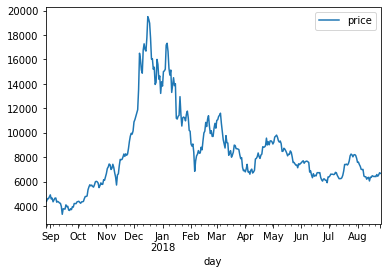
4.1.2 ARIMA 분석 방법
(2,1,2)
AR이 몇 번 째 과거까지를 바라보는지에 대한 파라미터(2)
차분Difference에 대한 파라미터 (1)
MA가 몇 번째 과거까지를 바라보는지에 대한 파라미터(2)
차분이란 현재 상태의 변수에서 바로 전 상태의 변수를 빼주는 것을 의미 (시계열 데이터의 불 규칙성을 조금이나마 보정해주는 역할을 함)
from statsmodels.tsa.arima_model import ARIMA
import statsmodels.api as sm
model = ARIMA(bitcoin_df.price.values,order=(2,1,2))
model_fit=model.fit(trend='c',full_output=True,disp=True)
print(model_fit.summary())
실행 결과를 분석해보았을 때 상수항을 제외한 모든 계수의 p-value가 0.05 이하로 나타난다. 이는 유의미한 값이라는 것을 알 수 있으며 AR과 MA 모두 2로 설정하는 것이 꽤 의미있는 분석결과라고 할 수 있다. ‘P > z’ 값이 일반적으로 학습의 적정성을 위해 확인되는 t-test값이다.
-> 음 완벽히 이해가 되지는 않는다 다른 파라미터에는 어떤게 있지 왜 0.05 이하가 적합한 값이라는 기준이 되는거지
const는 0.05 값에서 봤을 때 유효하지 않은데 그럼 파라미터 값을 nc로 바꿔야 하는건가?
https://byeongkijeong.github.io/ARIMA-with-Python/
ARIMA, Python으로 하는 시계열분석 (feat. 비트코인 가격예측)
서론 시계열 분석(Time series analysis)이란, 독립변수(Independent variable)를 이용하여 종속변수(Dependent variable)를 예측하는 일반적인 기계학습 방법론에 대하여 시간을 독립변수로 사용한다는 특징이
byeongkijeong.github.io
이 블로그를 보니 constraint가 없는 모형으로 fitting하면 MA(1)의 t-test값이 더 좋아졌다는데 내 모델은 어떤가
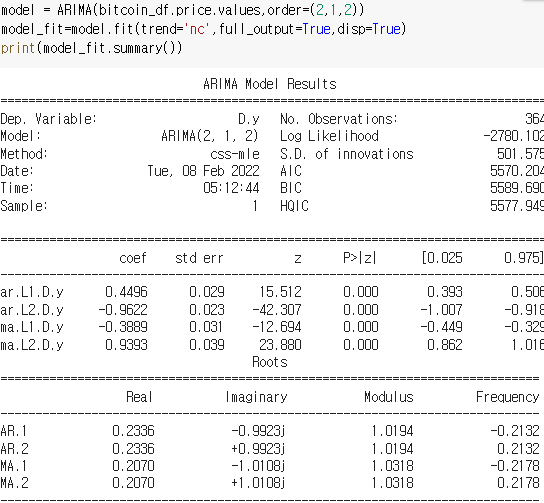
파라미터 값을 c로 설정한거랑 nc로 설정한거랑 뭐가 다른걸까 (의문)
0.000->0.000으로 같아서 nc나c나 상관없나?
모르겠다.. t-test값이 작을수록 좋은건 확실해
fig=model_fit.plot_predict() # 학습 데이터에 대한 예측 결과입니다. (첫 번째 그래프)
residuals=pd.DataFrame(model_fit.resid) # 잔차의 변동을 시각화합니다. (두 번째 그래프)
residuals.plot()

두 번째 그래프는 실제값과 예측값 사이의 오차 변동을 나타내는 그래프이다. 만약 이 그래프의 폭이 일정하다면 좋은 예측 모델을학습시킨 것이라고 생각 할 수 있다. 하지만 이 실행 결과에서는 오차 변동이 매우 불안정한 것으로 보인다.
4.1.3 ARIMA 모델 평가 : 실제 데이터와의 비교
모델을 평가하기 위해서는 테스트 전용 데이터가 필요한데 이번 예제에서는 5일 동안의 미래를 테스트 데이터로 사용한다. 불규칙적 시계열 예측의 경우에는 먼 미래를 예측하는 것이 큰 의미가 없으므로 ‘앞으로 N일 동안 어느정도로 상승/하락할 것 이다’ 정도의 대략적인 경향 예측만을 수행하는 것이 일반적이기 때문이다.
모델 평가 과정은 다음과 같다.
1. model_fit.forecast(steps=5)로 향후 5일의 가격을 예측하여 pred_y로 정의
2. ‘../data/market—price—test.csv’에서 실제 향후 5일의 가격을 test_y로 정의
3. 모델이 예즉한 상한값, 하한값을 pred_y_upper, pred_y_lower로 정의
4. 정의한 모든 값을 비교하여 5일 동안의 상승 경향 예측이 얼마나 맞았는지를 평가
forecast_data=model_fit.forecast(steps=5) #학습데이터셋으로 부터 5일 뒤를 예측합니다.
#테스트 데이터 셋을 불러옵니다.
test_file_path='/content/market-price-test.csv'
bitcoin_test_df=pd.read_csv(test_file_path,names=['ds','y'])
print(bitcoin_test_df)
pred_y=forecast_data[0].tolist() # 마지막 5일의 예측 데이터
test_y=bitcoin_test_df.y.values # 실제 5일 가격 데이터
pred_y_lower=[] #마지막 5일의 예측 데이터의 최소값
pred_y_upper=[] #마지막 5일의 예측 데이터의 최대값
for lower_upper in forecast_data[2]:
lower = lower_upper[0]
upper = lower_upper[1]
pred_y_lower.append(lower)
pred_y_upper.append(upper)
plt.plot(pred_y,color='gold') #모델이 예측한 가격 그래프
plt.plot(pred_y_lower,color='red') #모델이 예측한 최저 가격 그래프
plt.plot(pred_y_upper,color='blue') #모델이 예측한 최고 가격 그래프
plt.plot(test_y,color='green') #실제 가격 그래프이를 그래프로 시각화한 것은 다음과 같다.
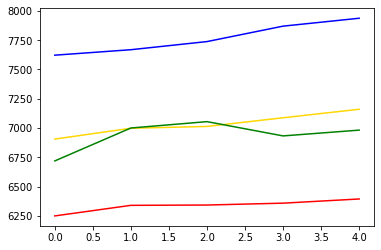
파란색 그래프는 모델이 예상한 최고 가격, 즉 상한가의 그래프, 그리고 빨간색은 모델이 예측한 하한가 그래프, 초록색은 실제 5일 간의 가격 그래프, 노란색은 모델이 예측한 5일간의 가격 그래프를 나타낸 것이다.

이번에는 상한가와 하한가를 제외한 뒤, 그래프를 살펴보았다. 그래프의 상승 경향을 살펴보면 그다지 좋지 않은 예측을 한 것으로 보인다. 하지만 ‘5일 동안 상승할 것이다’라는 아주 큰 트렌드 정도는 예측할 수 있다.

4.2.1 Facebook Prophet
다음으로 ARIMA보다 조금 더 정확한 트렌드 예측 분석을 제공하는 라이브러리 ‘Facebook Prophet’을 사용한다. Prophet은 Additive 모델이라는 모델링 방법에 기반한 시계열 예측 모델로서 시계열 데이터의 트렌드성 (연간/월간/일간)을 예측하는 것에 초점이 맞추어져 있다.
Additive 모델은 선형 회귀 분석의 단점을 극복하기 위해 개량된 분석 방법의 하나입니다. 시계열 분석 역시 회귀 분석의 한 갈래이기 때문에 회귀 분석의 단점을 가지고 있다. 하지만 회귀 분석의 단점을 극복하기 위해 이 모델은 각 피처마다 비선형적 적합을 가능하게 하는 일련의 방법을 적용한다.
# 5일을 내다보며 예측합니다
future_data=prophet.make_future_dataframe(periods=5,freq='d')
forecast_data=prophet.predict(future_data)
forecast_data.tail(5)학습 데이터셋 기반의 5일 단위 예측 데이터를 얻을 수 있다. 실행 결과는 데이터에 존재하지 않는 5일 단위의 미래를 예측한 것이다.

4.2.2 prophet 모델 시각화
prophet 모델의 학습 결과를 시각화한 결과이다. 그래프의 검은 점은 실제 가격을 나 타낸 것이고, 파란 선은 예측 가격을 나타낸 것이다. 이 모델 역시 ARIMA 모델과 마찬가지로 학습 데이터셋에 대해서는 거의 정확한 예측을 하고 있지만 시계열 데이터 분석에서 학습 데이터를 잘 예측하는 것은 큰 의미가 없다고 할 수 있다. 이미 답을 알고있는 모델이 데이터를 예측하는 행위는 의미가 없기 때문이다.
아래는 fbprophet에서 제공하는 트렌드 정보 시각화 그래프이다. year, weekly, daily 순의 트렌드를 확인할 수 있다.
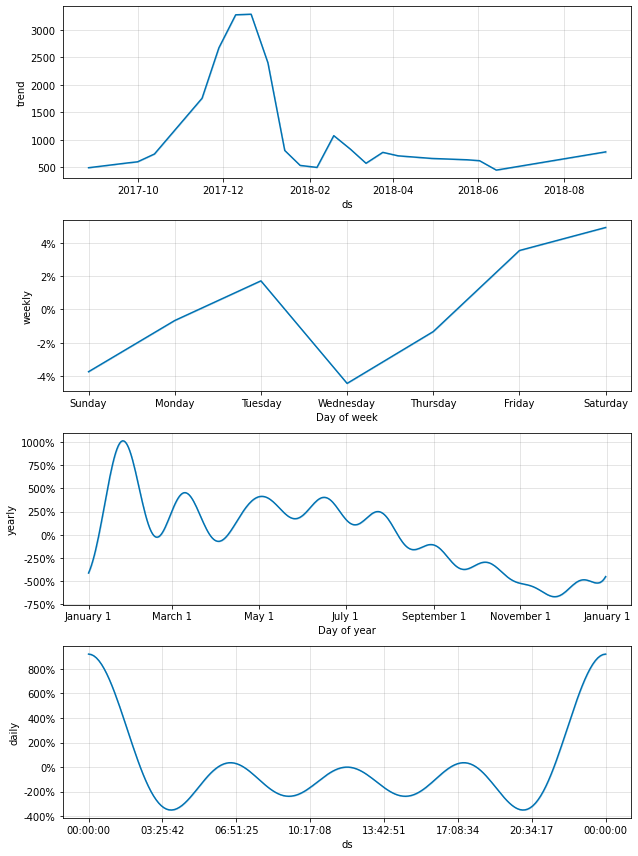
4.3.1 모델의 성능
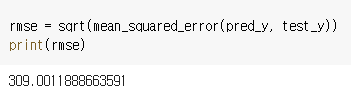
실제 가격과 예측한 가격간의 차이 : 첫 5일과 마지막 5일은 제외하고 계산한다.
y = bitcoin_df.y.values[5:] # 첫 5일을 제외한 실제 가격 데이터입니다.
y_pred = forecast_data.yhat.values[5:-5] # 첫 5일, 마지막 5일을 제외한 예측 가격 데이터입니다.
bitcoin_test_df = pd.read_csv(test_file_path, names=['ds', 'y'])
pred_y = forecast_data.yhat.values[-5:] # 마지막 5일의 예측 데이터입니다. (2018-08-27 ~ 2018-08-31)
test_y = bitcoin_test_df.y.values # 실제 5일 가격 데이터입니다. (2018-08-27 ~ 2018-08-31)
pred_y_lower = forecast_data.yhat_lower.values[-5:] # 마지막 5일의 예측 데이터의 최소값입니다.
pred_y_upper = forecast_data.yhat_upper.values[-5:] # 마지막 5일의 예측 데이터의 최대값입니다.plt.plot(pred_y, color="gold") # 모델이 예상한 가격 그래프입니다.
plt.plot(pred_y_lower, color="red") # 모델이 예상한 최소가격 그래프입니다.
plt.plot(pred_y_upper, color="blue") # 모델이 예상한 최대가격 그래프입니다.
plt.plot(test_y, color="green") # 실제 가격 그래프입니다.
plt.plot(pred_y, color="gold") # 모델이 예상한 가격 그래프입니다.
plt.plot(test_y, color="green") # 실제 가격 그래프입니다.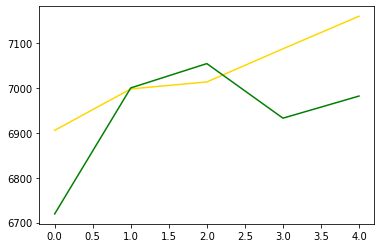

4.4.1 활용: 더 나은 결과를 위한 방법
모델의 성능을 조금 더 향상시킬 수 있는 방법은 뭐가 있을까? 첫 번째로 고려할 방법은 상한값 혹은 하한값을 지정해 주는 것이다. 바닥과 천장이 없는 주가 데이 터의 경우에는 의미가 없을 수 있지만 일반적인 시계열 데이터에서는 상한값 혹은 하한값을 설정해 주는 것이 모델의 성능을 높여줄 수 있는 방법 중 하나이다.
다른 방법은 이상치 제거 기법이다. 이상치란 평균적인 수치에 비해 지나치게 높거나 낮은 수치의 데이터를 의미한다. 예를들어, 상자 그림의 울타리 밖 영역에 있는 데이터들을 이상치 데이터라고 한다.
4.4.2 상한가 및 하한가 설정하기
bitcoin_df = pd.read_csv(file_path, names=['ds', 'y'])
# 상한가를 설정합니다.
bitcoin_df['cap'] = 20000
# 상한가 적용을 위한 파라미터를 다음과 같이 설정합니다.
prophet = Prophet(seasonality_mode='multiplicative',
growth='logistic',
yearly_seasonality=True,
weekly_seasonality=True, daily_seasonality=True,
changepoint_prior_scale=0.5)
prophet.fit(bitcoin_df)
# 5일을 내다보며 예측합니다.
future_data = prophet.make_future_dataframe(periods=5, freq='d')
# 상한가를 설정합니다.
future_data['cap'] = 20000
forecast_data = prophet.predict(future_data)
fig = prophet.plot(forecast_data)
예측과 실제 비교 그래프는 다음과 같다.
bitcoin_test_df = pd.read_csv(test_file_path, names=['ds', 'y'])
# 모델이 예상한 마지막 5일의 가격 데이터를 가져옵니다.
pred_y = forecast_data.yhat.values[-5:]
test_y = bitcoin_test_df.y.values
pred_y_lower = forecast_data.yhat_lower.values[-5:]
pred_y_upper = forecast_data.yhat_upper.values[-5:]
plt.plot(pred_y, color="gold") # 모델이 예상한 가격 그래프입니다.
plt.plot(pred_y_lower, color="red") # 모델이 예상한 최소가격 그래프입니다.
plt.plot(pred_y_upper, color="blue") # 모델이 예상한 최대가격 그래프입니다.
plt.plot(test_y, color="green") # 실제 가격 그래프입니다.
예측 모델이 형편없는 결과를 예측했다는 것을 알 수 있다. 모델이 예측한 상한가보다 실제 가격이 더 높기 때문이다. 게다가 이번에는 ‘5일 동안 상승/하락할 것이다’라는 큰 범 위의 트렌드를 예측하는 것조차 실패했다. 상한가라는 개념이 큰 의미가 없는 비트코인 데이터 의 경우에는 상한선을 설정한 것이 오히려 독이 되었다고 볼 수 있다.
4.4.3 이상치 제거하기
이 코드에서는 18,000 이상을 이상치라고 설정하였다.
plt.plot(pred_y, color="gold") # 모델이 예상한 가격 그래프입니다.
plt.plot(test_y, color="green") # 실제 가격 그래프입니다.
# 18000 이상의 데이터는 이상치라고 판단
bitcoin_df = pd.read_csv(file_path, names=['ds', 'y'])
bitcoin_df.loc[bitcoin_df['y'] > 18000, 'y'] = None
# prophet 모델을 학습합니다.
prophet = Prophet(seasonality_mode='multiplicative',
yearly_seasonality=True,
weekly_seasonality=True, daily_seasonality=True,
changepoint_prior_scale=0.5)
prophet.fit(bitcoin_df)
# 5일단위의 미래를 예측합니다.
future_data = prophet.make_future_dataframe(periods=5, freq='d')
forecast_data = prophet.predict(future_data)
# 예측 결과를 그래프로 출력합니다.
fig = prophet.plot(forecast_data)
실제 데이터와의 비교
- 비트코인 데이터의 경우, 이상치를 제거함으로써 오히려 예측력이 다소 떨어지는 결과를 보였다.
- 모델의 정확도 스코어 측면에서는 떨어졌지만, 트렌드 예측의 측면에서는 다소 나은 모습을 보여줄 수도 있다.
bitcoin_test_df = pd.read_csv(test_file_path, names = ['ds', 'y']) # 모델이 예상한 마지막 5일의 가격 데이터를 가져옵니다. pred_y = forecast_data.yhat.values[-5:] test_y = bitcoin_test_df.y.values pred_y_lower = forecast_data.yhat_lower.values[-5:] pred_y_upper = forecast_data.yhat_upper.values[-5:] plt.plot(pred_y, color="gold") # 모델이 예상한 가격 그래프입니다. plt.plot(pred_y_lower, color="red") # 모델이 예상한 최소가격 그래프입니다. plt.plot(pred_y_upper, color="blue") # 모델이 예상한 최대가격 그래프입니다. plt.plot(test_y, color="green") # 실제 가격 그래프입니다.
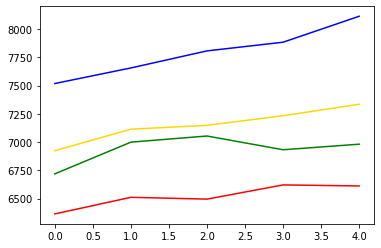
plt.plot(pred_y, color="gold") # 모델이 예상한 가격 그래프입니다.
plt.plot(test_y, color="green") # 실제 가격 그래프입니다
결과 : 이를 살펴본 결과, 이상치를 제거하는 것이 정확도(rmsE)면에서는 떨어지지만 ‘트렌드’를 예측하는 측면에서는 이전 모델보다 더 낫다고 볼 수 있다.